Programmation en Lua dans LaTeX : exemples concrets d'utilisation
par Damien Mégy latex lua lualatex maths
Table des matières
Introduction
Premiers exemples : tableaux de valeurs
On désire produire quelque chose du genre suivant (tableau mise en forme avec le package booktabs) :

Voici trois façons de parvenir à ce résultat :
\begin{tabular}{cc}\toprule
$n$ & $n^2$ \\ \midrule
\directlua{
for i=1,10 do
tex.print(i .. " & " .. (i^2) .. " \\\\")
end
}
\bottomrule\end{tabular}
Si l'on désire utiliser l'environnement luacode*, on ne peut pas le mettre à l'intérieur du tableau, il faut imprimer le début et la fin du tableau avec Lua :
\begin{luacode*}
tex.print("\\begin{tabular}{cc}\\toprule")
tex.print("$n$ & $n^2$ \\\\ \\midrule")
for i=1,10 do
tex.print(i .. " & " .. (i^2) .. " \\\\")
end
tex.print("\\bottomrule\\end{tabular}")
\end{luacode*}
Enfin, dans certains cas il peut être utile de fabriquer un tableau avec toutes les lignes à écrire, puis d'imprimer toutes les lignes à la fin en une seule fois.
\begin{luacode*}
local lines={}
lines[#lines+1] = "\\begin{tabular}{cc}\\toprule"
lines[#lines+1] = "$n$ & $n^2$ \\\\ \\midrule"
for i=1,10 do
lines[#lines+1] = i .. " & " .. (i^2) .. " \\\\"
end
lines[#lines+1] = "\\bottomrule\\end{tabular}"
-- impression :
for k=1,#lines do tex.print(lines[k]) end
\end{luacode*}
Note : dans ce cas précis, tex.print(table.concat(lines,"\n")) produit une erreur car TeX ne comprend pas les sauts de ligne Lua et que l'environnement tabular est pénible avec ça.
Plutôt qu'utiliser l'opérateur de concaténation, on peut utiliser string.format() pour imprimer les lignes. Ceci permet aussi d'imprimer les entiers comme des entiers, sans décimales.
\begin{luacode*}
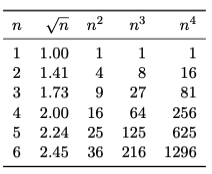
tex.print("\\begin{tabular}{crrrr} \\toprule")
tex.print("$n$ & $\\sqrt{n}$ & $n^2$ & $n^3$ & $n^4$ \\\\ \\midrule")
for n=1,6 do
tex.print(
string.format("%d & %.2f & %d & %d & %d \\\\",
n, math.sqrt(n), n^2, n^3, n^4)
)
end
tex.print("\\bottomrule\\end{tabular}")
\end{luacode*}
Ceci produit la table:
Exemples plus avancés
Les exemples précédents sont facilement faisables sans Lua. Les suivants seraient un peu plus pénibles à coder en TeX, là où leur implémentation en Lua reste très claire à lire.
Diviseurs, décompositions en facteurs premiers
Dans un bloc luacode :
\begin{luacode*}
function divisors(n)
local t={}
for i=2,n do
if n % i == 0 then
table.insert(t, i)
end
end
return t
end
\end{luacode*}
\newcommand\listOfDivisors[1]{%
\directlua{tex.print(table.concat(divisors(#1),","))}
}
Les diviseurs positifs de $60$ sont \listOfDivisors{60}.
(On peut ensuite adapter le code pour gérer les entiers négatifs.)
Prochain nombre premier
\begin{luacode*}
function is_prime(n)
if n < 2 then return false end
for i=2,math.floor(math.sqrt(n)) do
if n % i == 0 then return false end
end
return true
end
function next_prime(n)
while not is_prime(n) do
n = n+1
end
return n
end
\end{luacode*}
\newcommand{\nextPrime}[1]{\directlua{tex.sprint(next_prime(#1))}}
Le prochain nombre premier après 1000 est \nextPrime{1000}.
% affiche 1009
Décompositions en facteurs premiers
Dans le préambule :
\begin{luacode*}
function factor(n)
local t, d = {}, 2
while n > 1 do
while n % d == 0 do
t[#t+1] = d
n = n / d
end
d = d + 1
end
return t
end
\end{luacode*}
\newcommand{\factor}[1]{\directlua{tex.sprint(table.concat(factor(#1),"\\times"))}}
Ensuite:
Décompositions en produit de facteurs premiers :
\begin{itemize}
\item $17 = \factor{17}$.
\item $60 = \factor{60}$. %% affiche 2x2x3x5
\item $720 = \factor{720}$.
\item $160 = \factor{160}$.
\end{itemize}
Remarque : on peut relativement facilement modifier la fonction pour qu'elle affiche $2^2\times 3\times 5$ au lieu de $2\times 2 \times 3 \times 5$.
Calculs de PGCD
Tout d'abord, une fonction de pgcd en Lua et la macro correspondante en LaTeX :
\begin{luacode*}
function gcd(a,b)
while b ~= 0 do
a, b = b, a % b
end
return math.abs(a)
end
\end{luacode*}
\newcommand\mathgcd[2]{
\directlua{tex.sprint(gcd(#1,#2))}
}
Test : le pgcd de $-4$ et $14$ est $\mathgcd{-4}{14}$.
% affiche 2
On a nommé la macro \mathgcd et non \pgcd ou \gcd car en général il y a déjà un opérateur pgcd ou gcd défini dans la feuille de style avec Declaremathoperator.
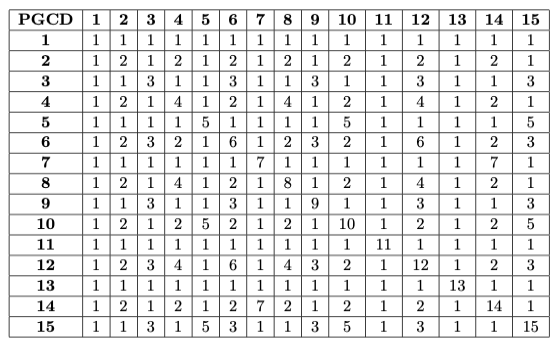
Avec très peu de code, on peut alors afficher facilement le tableau suivant qui récapitule tous les pgcd des nombres inférieurs à 15 :
Écriture de nombres en base b
L'objectif ici est de pouvoir écrire dans son fichier texte la chose suivante :
Le nombre $255$ en base $16$ s'écrit \tobase{255}{16}. % affiche "FF"
Le nombre $13$ en base $2$ s'écrit \tobase{13}{2}. % affiche "1101"
Pour cela, on définit la macro LaTeX \tobase{}{} de la façon suivante :
\newcommand{\tobase}[2]{%
\directlua{tex.print(toBase(#1, #2))}%
}
et on définit la fonction Lua toBase(n,b) comme ceci :
function toBase(n, b)
assert(b >= 2 and b <= 36, "La base b doit être entre 2 et 36")
assert(n >= 0, "L'entier n doit être positif")
if n == 0 then
return "0"
end
local digits = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"
local result = ""
while n > 0 do
result = digits:sub((n % b) + 1, (n % b) + 1) .. result
n = n // b
end
return result
end
Ou encore, en version récursive :
local digits = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"
function toBase(n, b)
assert(b >= 2 and b <= 36, "La base b doit être entre 2 et 36")
assert(n >= 0, "L'entier n doit être positif")
if n < b then
return digits:sub(n + 1, n + 1)
end
return toBase(n // b, b)
.. digits:sub((n % b) + 1, (n % b) + 1)
end
Table de nombres premiers jumeaux
Comme dernier exemple, on montre comment obtenir la table suivante, qui affiche les nombres premiers jumeaux inférieurs à N (avec N=100 dans cet exemple):

\begin{luacode*}
local N=100
local is_prime = {false}
for i=2,N do
if is_prime[i] == nil then
is_prime[i]=true
for j=2*i,N,i do
is_prime[j] = false
end
end
end
tex.print("\\begin{tabular}{cc} \\toprule")
tex.print("p premier & p+2 premier jumeau \\\\ \\midrule")
for n=2,N do
if is_prime[n] and is_prime[n+2] then
tex.print(string.format("%d & %d \\\\", n, n+2))
end
end
tex.print("\\bottomrule\\end{tabular}")
\end{luacode*}
Conclusion
Programmer en Lua dans LaTeX en compilant avec le moteur LuaLaTeX est facile et amusant. On peut réussir à faire des choses qu'on n'aurait jamais eu le courage de faire avec LaTeX seul et pgf, surtout avec l'aide d'une intelligence artificielle, qui est bien plus efficace pour déboguer Lua que du TeX de bas niveau ou un obscur package en PsTricks.
Un certain nombre d'exemples présentés plus haut sont en fait directement disponibles dans certains packages LuaLaTeX, donc il n'y a en fait pas besoin de recoder toutes les fonctions de pgcd etc: elles existent souvent déjà.