Visualiser les symétries de l'octaèdre régulier en LaTeX avec TikZ (3d)
par Damien Mégy latex tikz 3d maths polytopes
Table des matières
L'octaèdre régulier est l'un des cinq solides de Platon. Le gif animé ci-dessous est tiré de Wikipedia:
Cette animation présente un octaèdre en rotation, mais l'axe a été choisi au hasard et n'est pas un axe de rotation «naturel» de l'octaèdre.
Dans cet article, on passe en revue certaines façons de tracer des octaèdres en LaTeX et d'exporter des animations sous forme de gif animé ou pdf animé. Le but est de visualiser efficacement les axes de rotation naturels comme dans les animations ci-dessous, dont le code est disponible plus bas.
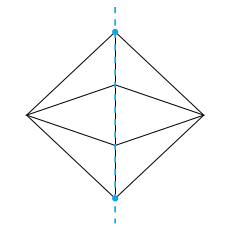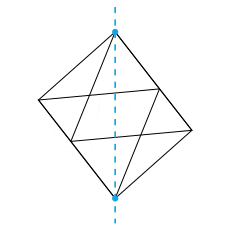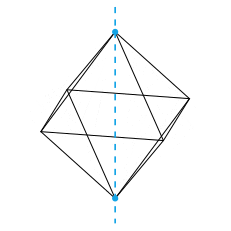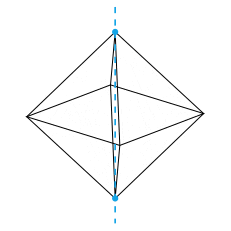
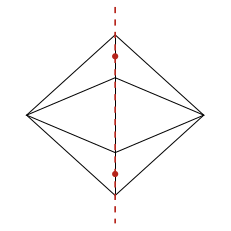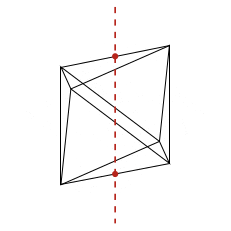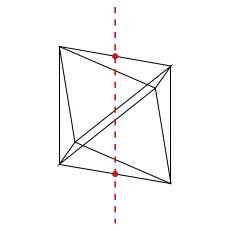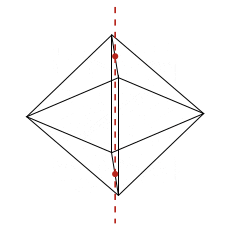
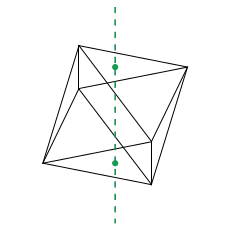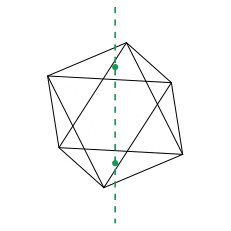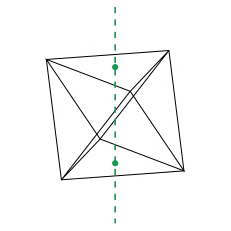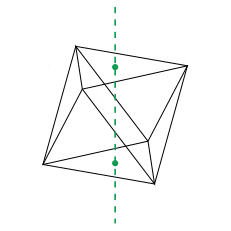
Les rotations de l'octaèdre régulier
Il y a 24 rotations 3d qui laissent l'octaèdre régulier globalement invariant, en comptant l'identité. Une première liste, faisant apparaître l'angle de la rotation, et le nombre de telles rotations, est la suivante :
| angle de la rotation | quantité de telles rotations |
|---|---|
| 0° | 1 |
| ±120° | 8 |
| 180° | 9 |
| ±90° | 6 |
Le total est bien 24. Cependant ce tableau ne donne que peu d'informations sur la nature géométrique de ces rotations et peut même induire en erreur. Il y a en effet plusieurs types de rotations de 180°, avec des axes de nature différente.
Pour mieux comprendre tout ceci, traçons quelques figures.
La 3D dans tikZ
Le package TikZ permet de déclarer des points en 3d en donnant leurs coordonnées cartésiennes, par exemple \coordinate (N) at (0,0,1);
On va donc définir une nouvelle commande qui déclare les six sommets de l'octaèdre, et qui dessie toutes les arêtes. Cette commande pourra ensuite être utilisée à l'intérieur d'un environnement tikzpicture.
\usepackage{tikz}
\usepackage{tikz-3dplot} % pour plus tard
\newcommand{\drawOctahedron}{%
\coordinate (N) at (0,0,1);
\coordinate (S) at (0,0,-1);
\coordinate (A) at (1,0,0);
\coordinate (B) at (0,1,0);
\coordinate (C) at (-1,0,0);
\coordinate (D) at (0,-1,0);
\draw (N) -- (A) -- (S) -- (C) -- cycle;
\draw (N) -- (B) -- (S) -- (D) -- cycle;
\draw (A) -- (B) -- (C) -- (D) -- cycle;
}
Ensuite, le code \tikz{\drawOctahedron} produit la figure suivante:
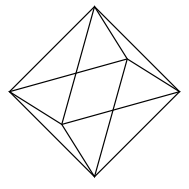
Tikz a projeté l'octaèdre sur un plan avec une projection arbitraire.
Si l'on veut projeter le solide d'une autre façon, c''est possible mais il faut préciser la projection, c'est-à-dire les coordonnées planaires des trois vecteurs (1,0,0), (0,1,0) et (0,0,1) dans l'espace.
Ceci se fait de la façon suivante :
\begin{tikzpicture}[x={(4cm,-4cm)}, y={(-5cm,3cm)}, z={(5cm,4cm)}]
\drawOctahedron
\end{tikzpicture}
Le résultat est le suivant :
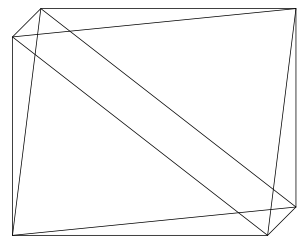
Un peu immonde ? C'est normal, il faut éviter de choisir les paramètres de projection [x={(4cm,-4cm)}, y={(-5cm,3cm)}, z={(5cm,4cm)}] au hasard... Les trois vecteurs doivent former les deux premières lignes d'une matrice 3x3 orthogonale, sinon tout est déformé.
Écrire à la main les entrées d'une matrice orthogonale est pénible. On pourrait les calculer (voir par exemple les formules sur wikipedia), mais dans ce cas il serait préférable d'utiliser Lualatex. Une autre solution est de chercher un package proposant déjà ces fonctionnalités.
Le package tikz-3dplot
Le package tikz-3dplot permet de changer les coordonnées plus facilement qu'en entrant la matrice de projection à la main.
On peut par exemple entrer les coordonnées sphériques, en degrés, avec \tdplotsetmaincoords{colatitude}{longitude}. La colatitude $\theta$ est une mesure de la latitude qui commence à 0° au pôle nord, vaut 90° à l'équateur et atteint 180° au pôle sud. Une colatitude de zéro correspond à une vue "du dessus" (on regarde le pôle nord "depuis le haut").
Colatitude $\theta$ et longitude $\phi$. Image : Wikipedia.
À titre d'exemple, la ville de Paris se trouve aux coordonnées géographiques approximatives suivantes : Latitude : 49° Nord; Longitude : 2° Est. Ceci correspondrait donc à une colatitude de 90°-49° = 41°.
Une fois qu'on a fixé le point de vue en sphériques avec la commande \tdplotsetmaincoords{}{}, on peut dessiner l'octaèdre en précisant la projection: \begin{tikzpicture}[tdplot_main_coords] ... \end{tikzpicture}.
On peut aussi tracer l'octaèdre depuis une multitude de points de vue sur une même figure:
\begin{tikzpicture}[scale=2]
\foreach \i in {0,15,...,45}{%
\foreach \j in {0,15,...,45}{%
\tdplotsetmaincoords{\i}{\j}
\begin{scope}[shift={(\i/7,\j/7)},tdplot_main_coords]
\drawOctahedron
\end{scope}
}
}
\end{tikzpicture}

Cette image fait apparaître plusieurs choses intéressantes:
- La colonne de gauche montre l'octaèdre vu "depuis un sommet". L'observateur voit alors quatre faces de l'octaèdre et la figure tracée est un carré.
- La figure en bas à droite montre l'octaèdre vu "face à une arête" : l'observateur ne voit alors que deux faces de l'octaèdre et la figure tracée est un losange. Attention, les deux triangles qui forment ce triangle ne sont pas exactement équilatéraux puisque les deux faces sont vues de biais.
- Sur la figure en haut à droite, on voit deux triangles presque équilatéraux avec des orientations opposées. Les triangkes ne sont pas équilatéraux car là non plus, on n'est pas tout à fait dans l'axe des faces. D'ailleurs, l'hexagone que l'on voit n'est pas régulier. (Voir plus bas pour un alignement parfait avec les faces.)
On distingue ainsi des rotations de 90°, 180° et 120° qui laissent l'octaèdre invariant.
Les axes de rotation
Six axes «de type 2» passant par les milieux d'arêtes opposées
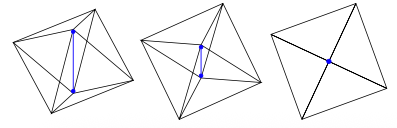
L'octaèdre a 12 arêtes, donc 6 paires d'arêtes opposées. Les droites passant par les milieux de deux arêtes opposées sont des axes de rotation de l'octaèdre, pour un angle de 180° (demi-tour). Ces axes sont du type ci-dessous.
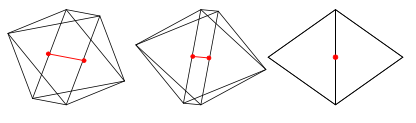
Quatre axes «de type 3» passant par les centres de deux faces opposées
L'octaèdre a huit faces, dont quatre couples de faces opposées.
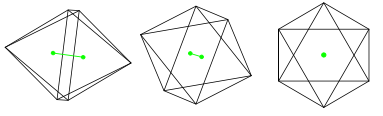
Trois axes «de type 4» passant par deux sommets opposés
L'octaèdre a six sommets, donc trois couples de sommets opposés.
Liste des rotations
La liste complète des rotations de l'octaèdre, un peu plus détaillées que la précédente, est finalement :
| angle | nombre | type d'axe | Remarque |
|---|---|---|---|
| 0° | 1 | - | |
| ±120° | 2x4=8 | type 3 | 4 paires de faces opposées |
| 180° | 3 | type 4 | 3 paires de sommets opposés |
| 180° | 6 | type 2 | 6 paires d'arêtes opposées |
| ±90° | 2x3=6 | type 4 | 3 paires de sommets opposés |
Création de gifs animés
Pour créer un gif animé comme celui en haut de la page, il y a en général deux étapes:
- création d'un pdf avec toutes les images (une par page);
- création d'un gif animé à partir du pdf.
Pour l'étape 1:
\documentclass[multi,tikz]{standalone}
\usepackage[dvipsnames]{xcolor}
\usepackage{tikz-3dplot}
\newcommand{\drawOctahedron}{%
% - - - comme auparavant - - -
}
\begin{document}
\foreach \i in {0, 3, ..., 87}{
\tdplotsetmaincoords{70}{\i}
\begin{tikzpicture}[scale=1.5, tdplot_main_coords]
\fill[white] (0,0,0) circle (1.3cm);
\drawOctahedron
\draw[Cerulean, thick, dashed] (0,0,1.3) -- (0,0,-1.3);
\fill[Cerulean] (0,0,1) circle (1pt);
\fill[Cerulean] (0,0,-1) circle (1pt);
\end{tikzpicture}
}
\end{document}
Le disque blanc dessiné en fond sert juste à fixer les dimensions de l'image et à ne pas avoir de surprises avec le recadrage automatique.
Ensuite, il faut créer le gif animé.
La première solution est d'utiliser imagemagick (qui lui-même utilise ghostscript)
magick -density 150 file.pdf -background white -alpha remove -alpha off -loop 0 -delay 3 file.gif
Explication : -density 150 pour une résolution de 150 pixels par pouce, -loop 0 pour une lecture en boucle, -delay 3 pour 3 ms par image (donc 33 images/s). Attention à l'ordre des options. Note : auparavant, on utilisait convert mais la commande est dépréciée depuis Imagemagick version 7 et on utilise magick à la place.
Cependant, la conversion pdf vers bitmap n'est pas très bonne en présence de lignes fines, et le gif animé produit n'a pas forcément la vitesse annoncée. Une autre solution, recommandée, est la suivante :
pdftocairo -png -r 150 file.pdf frame
gifski frame-*.png --fps 50 -o file.gif
La première commande produit des images frame-1.png, frame-2.png etc. La seconde produit le fichier .gif. On peut ensuite nettoyer avec rm frame-*.png, si besoin.
Résultat:

Si les outils ci-dessus ne sount pas installé : brew install gifski, brew install gs, brew install imagemagick etc.
Pour les autres axes de rotation, le plus simple est de garder un axe vertical et de modifier les coordonnées des sommets de l'octaèdre :
\coordinate (N) at (1,0,0);
\coordinate (S) at (-1,0,0);
\coordinate (A) at (0,.707,.707);
\coordinate (B) at (0,.707,-.707);
\coordinate (C) at (0,-.707,-.707);
\coordinate (D) at (0,-.707,.707);
et, pour le troisième type d'axe :
\def\r{sqrt(2)/sqrt(3)}
\coordinate (N) at ({\r},0,{sqrt(3)/3});
\coordinate (A) at ({\r*cos(120)},{\r*sin(120)},{sqrt(3)/3});
\coordinate (B) at ({\r*cos(-120)},{\r*sin(-120)},{sqrt(3)/3});
\coordinate (S) at ({-\r},0,{-sqrt(3)/3});
\coordinate (C) at ({\r*cos(-60)},{\r*sin(-60)},{-sqrt(3)/3});
\coordinate (D) at ({\r*cos(60)},{\r*sin(60)},{-sqrt(3)/3});

